Загрязнение питьевой воды из года в год остаётся одной из главных проблем во многих городах России, поэтому задача установления и оценки связи между качеством воды и показателями заболеваемости с целью принятия управленческих решений, остается актуальной.

Целью исследования являлось изучение влияния химического состава воды на заболеваемость детей. В качестве исходной информации были использованы ретроспективные данные о присутствии примесей и веществ в питьевой воде, а также данные о заболеваемости детей, зарегистрированной в детских поликлиниках города за период с 1995 по 2005 г.

Задачами исследования явились:

1. анализ взаимозависимости факторов модели (показателей качества питьевой воды) и зависимых переменных (заболеваемости);

2. построение математических моделей зависимости заболеваемости от факторов;

3. моделирование детской заболеваемости;

4. формирование заключений о влиянии химического состава воды на заболеваемость детей.

Рассматривались следующие нозологии (зависимые переменные) и показатели химического состава воды (факторы):

Таблица 1

Перечень нозологий

Таблица 2

Перечень показателей химического состава воды

Любое исследование начинается со спецификации модели, т. е. с формулировки вида модели, исходя из соответствующей теории связи между переменными. Иными словами, исследование начинается с теории, устанавливающей связь между явлениями.

Ставя цель дать количественное описание взаимосвязей между переменными, прежде всего, применяются методы регрессии и корреляции.

Для решения первой из поставленных задач мы применили корреляционный анализ. Корреляционный анализ должен дать ответы на вопросы, какие из факторов , присутствующих в модели, существенно влияют на зависимую переменную, определить количественную меру этого влияния и, поскольку процесс случайный, оценить достоверность полученных результатов. Отобранные таким образом факторы  включаются в регрессионную модель для исследований.

Корреляционный анализ, проведенный для данных о заболеваемости детей, показал наличие корреляционной связи на уровне 0,05, (адекватность подтверждена при помощи критерия Стьюдента) для следующих заболеваний и химических элементов, наблюдаемых в составе воды.

Таблица 3

Результаты корреляционного анализа

Кроме того, показатели количества марганца и жесткости воды значимо коррелируют друг с другом (0,719; 4,069), следовательно, при построении моделей один из этих факторов исключался.

На втором этапе работы мы определяли вид модели, принимая во внимание структуру и особенности экспериментальных данных. В качестве основных видов моделей были рассмотрены регрессионные (парные и множественные, линейные и нелинейные) модели, самоорганизационные полиномиальные модели, построенные при помощи метода группового учета аргументов (МГУА), нейросетевые модели.

Выбор был остановлен на регрессионных и МГУА-моделях. Указанные виды моделей предъявляют требования к факторам, включаемым в модель. МГУА пытается построить модель таким образом, чтобы предсказанное значение выхода было как можно ближе к истинному значению, генерируя легкую для понимания полиномиальную модель. В программе MS Excel нами были построены парные линейные и нелинейные регрессионные модели, но ни одна их них не оказалась адекватной. МГУА-модели были построены при помощи программного пакета NeuroShell2. Модели оказались адекватными (согласно коэффициенту детерминации, корреляции, СКО, нормСКО).

На третьем этапе мы осуществили имитационное моделирование моделей по принципу Δt. Принцип Δt предполагает преобразование модели системы к такому виду, чтобы значения Z₁, Z₂, … Z_n в момент времени t₁= t₀ ± Δt можно было вычислить через начальные значения, а в момент t₂=t₁+± Δt через значения на предшествующем шаге и так для каждого i-ого шага (± Δt =const, i=1M).

Как пример рассмотрим имитационное моделирование показателя «Болезни эндокринной системы» в среде MathCAD. МГУА-модель включала в качестве факторов показатели количества фтора (х2), нитратов (х4) и марганца (х5) в воде: 

Мы изменяли значения одного из факторов, в то время, как остальные оставались неизменными (были взяты равными средним значениям).

Как видно на рис.1, увеличение содержания марганца в питьевой воде до уровня 0,4 сопровождается снижением количества заболевших, но дальнейший рост содержания марганца вызывает резкое возрастание количества заболевших детей.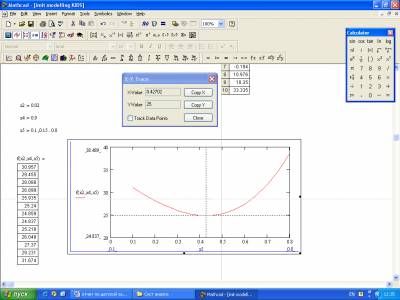

Рисунок 1– График изменения количества заболевших при изменении концентрации марганца в питьевой воде

Подобное изменение показателей количества фтора и нитратов сопровождалось снижением показателя заболеваемости, и не было отмечено ее явного изменения. Для нозологий, определенных в качестве индикативных, были построены имитационные модели, и исследованы в соответствии с примером, рис.1.

Результаты имитационного моделирования для всех построенных моделей приведены в табл.4. Нижеприведенные модели представлены без нормирующих

коэффициентов, которые рассчитываются в программном пакете NeuroShell 2, но отражают форму полинома и структуру модели.

Таблица 4

Фрагмент таблицы с построенными моделями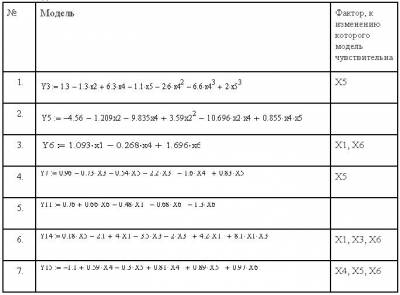

Как следует из произведенных вычислений и таблицы, нозологии Y3, Y7, Y15 являются чувствительными к фактору Х5 (марганец), причем минимальной концентрацией этого вещества, вызывающей рост независимой переменной, является значений 0,2 (0, 35 для Y7, 0,2 для Y15, 0,4 для Y3).

На нозологии «Болезни мочеполовой системы» Y12 и «Болезни кожи и подкожной клетчатки» Y14 оказывает негативное влияние присутствие железа в воде. Кроме того, значение Y14 увеличивается с увеличением жесткости воды и концентрации в ней нитритов. Количество «Болезней костно-мышечной системы» Y15 растет с ростом концентрации марганца, нитратов и жесткости воды (X4, X5, X6). «Болезни нервной системы» чувствительны к росту концентраций железа и к увеличению жесткости воды.

Выводы: проведенный анализ выявил присутствие действительной корреляционной зависимости между рядом нозологий и химическими составляющими воды.

На основе построенных МГУА-моделей были исследованы зависимости нозологий от изменения концентрации факторов, причем были определены концентрации веществ, способствующие резкому росту заболеваемости. Учитывая вышеизложенное, актуальным является проведение дальнейшего углубленного изучения влияния факторов окружающей среды на здоровье населения.